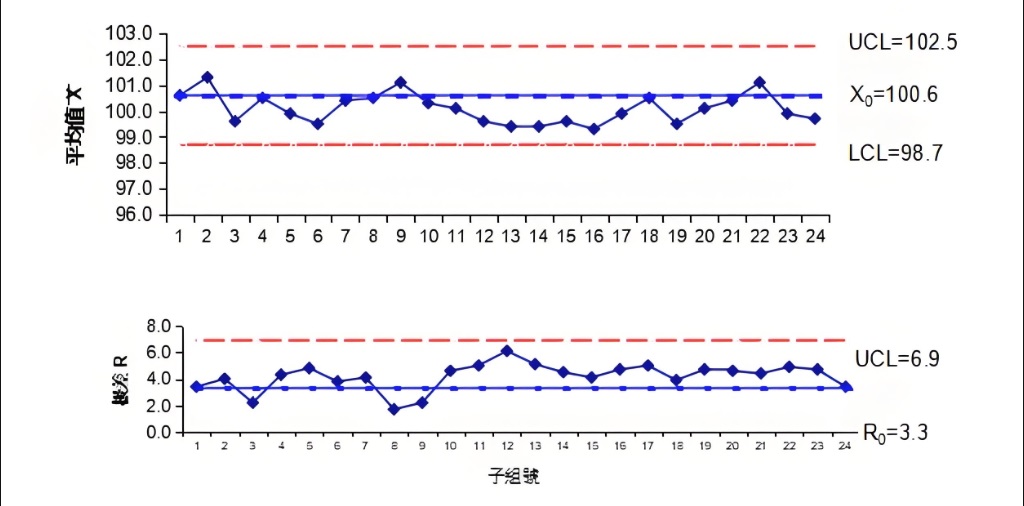
控制图
控制图(Control Chart)是统计过程控制(SPC)的核心工具,由美国贝尔实验室的休哈特(Walter Shewhart)博士于1924年提出。它通过可视化数据波动,区分生产过程中的正常波动(偶然原因)与异常波动(特殊原因),帮助企业实时监控质量、预防不良品、优化流程。
控制图的基本原理
核心逻辑
基于正态分布特性:若过程稳定,99.73%的数据应落在中心线±3σ(标准差)的控制限内。
判异规则:数据点超出控制限(UCL/LCL)或呈现特定分布模式(如连续上升/下降)时,表明存在异常原因。
两类错误风险
α风险(虚发警报):正常过程误判为异常(概率0.27%)。
β风险(漏发警报):异常过程误判为正常,导致不合格品增加。
控制限设为±3σ是为平衡两类风险的总损失最小化。
核心功能
过程监控:实时跟踪过程输出(如产品尺寸、服务响应时间等),判断是否处于统计控制状态。
异常检测:识别超出控制界限的点、趋势或模式,提示可能存在特殊原因(如设备故障、操作失误)。
持续改进:通过分析异常原因,优化过程参数,减少变异,提升质量水平。
控制图的核心要素
| 组成部分 | 作用 | 示例 |
|---|---|---|
| 中心线(CL) | 过程均值(如平均值、中位数) | 生产线瓶装容量平均值=500ml |
| 控制上限(UCL) | 均值+3倍标准差(99.73%数据应在此范围内) | UCL=505ml |
| 控制下限(LCL) | 均值-3倍标准差 | LCL=495ml |
| 数据点 | 按时间顺序排列的样本统计量(如单值、均值、极差等) | 每小时抽取5瓶测量容量 |
控制图类型及适用场景
控制图类型
根据数据类型和用途,控制图分为两大类:计量型和计数型。
计量型控制图(连续数据,如尺寸、温度)
X-bar & R图:监控过程均值(X-bar)和极差(R),适用于子组样本量较小(通常2-10)的场景。
X-bar & S图:用标准差(S)替代极差,适用于子组样本量较大(≥10)时。
I-MR图(单值-移动极差图):适用于无法分组的数据(如单件生产),通过移动极差分析变异。
| 类型 | 符号 | 适用场景 | 特点 |
|---|---|---|---|
| 均值-极差控制图 | X̄-R | 小样本(n=2~9) | 最常用,计算简单 |
| 均值-标准差控制图 | X̄-S | 大样本(n≥10) | 精度更高 |
| 单值-移动极差控制图 | X-Rs | 单件/慢速生产(每次仅1个数据) | 灵敏度低,但操作简便 |
| 中位数-极差控制图 | X̃-R | 数据非正态或含异常值 | 抗干扰强 |
计数型控制图(离散数据,如缺陷数、不合格率)
P图:监控不合格品率(比例),适用于样本量不固定的情况。
NP图:监控不合格品数量,要求样本量恒定。
C图:监控单位缺陷数(如每平方米瑕疵点数),适用于样本量恒定。
U图:监控单位缺陷率(如每百件缺陷数),适用于样本量不固定。
| 类型 | 符号 | 适用场景 |
|---|---|---|
| 不合格品率控制图 | P | 样本量不等(如抽检批次大小不同) |
| 不合格品数控制图 | nP | 样本量固定 |
| 缺陷数控制图 | C | 单位产品缺陷数(如纺织品瑕疵) |
| 单位缺陷数控制图 | U | 样本量不等时的缺陷密度监控 |
控制图适用场景
| 类型 | 适用数据 | 公式 | 典型案例 |
|---|---|---|---|
| X̄-R图(均值-极差) | 连续数据,子组大小≤10 | X̄=子组均值,R=子组极差 | 监控生产线零件尺寸稳定性 |
| X-MR图(单值-移动极差) | 连续数据,子组大小=1 | MR=相邻两数据点差值绝对值 | 化工反应温度监控(无法分组) |
| P图(不合格品率) | 二项分布数据(合格/不合格) | P=不合格品数/样本量 | 电子元件焊接不良率监控 |
| U图(单位缺陷数) | 泊松分布数据(缺陷计数) | U=缺陷数/单位 | 纺织品每平方米瑕疵数监控 |
计数型控制和计量型控制图的异同点
核心差异
| 维度 | 计数型控制图 | 计量型控制图 |
|---|---|---|
| 数据类型 | 离散数据(属性数据) | 连续数据(变量数据) |
| 监控对象 | 不合格品数、缺陷数等非数值型指标 | 长度、重量、温度等可测量的数值型指标 |
| 样本量要求 | 可变(如P图、U图)或固定(如NP图、C图) | 通常需分组(子组),样本量固定 |
| 控制界限计算 | 基于二项分布或泊松分布 | 基于正态分布 |
| 灵敏度 | 对小偏移的检测能力较弱 | 对小偏移的检测能力较强 |
| 应用场景 | 缺陷率、不合格品率监控 | 关键尺寸、性能参数监控 |
详细对比
1. 数据类型与监控对象
计数型控制图:
数据类型:离散数据,如“合格/不合格”“缺陷有无”。
监控对象:
不合格品率(P图、NP图):如每百件产品中的不合格品数。
缺陷数(C图、U图):如每平方米玻璃上的气泡数。
特点:数据简单,但信息量有限,无法反映偏差程度。
计量型控制图:
数据类型:连续数据,如长度、重量、时间等。
监控对象:
过程均值(X-bar图):如零件直径的平均值。
过程变异(R图、S图):如直径的极差或标准差。
特点:数据丰富,可捕捉微小偏移,但需测量系统精确。
2. 样本量与分组要求
计数型控制图:
样本量可变:如P图和U图允许每批样本量不同(如订单批量不一)。
样本量固定:NP图和C图要求每批样本量相同(如每小时抽检100件)。
分组灵活性:适用于非均匀生产过程。
计量型控制图:
需分组(子组):通常每组包含2-10个样本(如每班抽5件产品)。
样本量固定:子组大小需一致,以稳定控制界限计算。
适用场景:连续生产过程,如流水线作业。
3. 控制界限计算
计数型控制图:
基于概率分布:
P图/NP图:二项分布(不合格品率)。
C图/U图:泊松分布(缺陷数)。
公式示例(P图):
中心线(CL)= 历史不合格品率均值。
控制界限:UCL/LCL = CL ± 3√[CL(1-CL)/n](n为样本量)。
计量型控制图:
基于正态分布:
X-bar图:UCL/LCL = X̄ ± A₂R̄(A₂为常数,R̄为极差均值)。
R图:UCL/LCL = D₄R̄ / D₃R̄(D₃、D₄为常数)。
特点:需计算子组均值和变异,对数据分布敏感。
4. 灵敏度与异常检测
计数型控制图:
灵敏度较低:对过程偏移的检测需积累更多数据(如缺陷率需显著上升才能触发警报)。
适用场景:缺陷率稳定且较低的过程(如<5%)。
计量型控制图:
灵敏度较高:可检测均值或变异的微小偏移(如0.5σ shift)。
优势:提前预警,减少不合格品产生。
5. 应用场景示例
计数型控制图:
P图:监控手机组装线每日不合格品率(样本量随订单变化)。
U图:跟踪每台发动机的缺陷数(如密封圈漏装、螺丝松动)。
计量型控制图:
X-bar & R图:监控汽车轴承直径的均值和极差(每班抽5件,连续生产)。
I-MR图:监测单件定制产品的厚度(如航空航天零件)。
共同点
目的相同:均用于监控过程稳定性,区分普通原因与特殊原因变异。
控制界限逻辑:均采用±3σ原则设定UCL/LCL,覆盖99.73%的正常波动。
判异规则:均遵循Western Electric规则(如点超出界限、连续7点上升等)。
持续改进:通过分析异常点,推动过程优化。
选择建议
优先计量型控制图:
数据可量化且测量系统可靠。
需检测微小偏移或关键质量特性(CTQ)。
示例:半导体晶圆厚度、药品有效成分含量。
选择计数型控制图:
数据为离散属性(合格/不合格)。
测量成本高或无法连续测量(如破坏性测试)。
示例:食品包装密封性检测、软件缺陷率。
实践案例
案例1(计数型):
某电子厂使用P图监控电路板焊接不良率,发现连续8点低于中心线,调查后发现助焊剂浓度不足。
案例2(计量型):
某钢厂通过X-bar & R图监控钢板厚度,发现R图连续6点上升,检查轧机辊缝发现磨损。
总结
计数型控制图适用于离散、简单的缺陷监控,而计量型控制图更适合连续、精确的过程参数控制。实际应用中,可根据数据类型、测量成本和过程灵敏度需求综合选择,甚至结合使用(如先通过计量型图控制关键尺寸,再用计数型图监控最终合格率)。
构建步骤
数据收集:按时间顺序收集过程输出数据,分组(子组)或单值记录。
计算统计量:
计量型:计算子组均值(X-bar)、极差(R)或标准差(S)。
计数型:计算不合格品率(P)、不合格数(NP)、缺陷数(C/U)。
确定控制界限:
上控制限(UCL)= 中心线(CL) + 3×标准差(σ)。
下控制限(LCL)= 中心线(CL) - 3×标准差(σ)。
(CL通常为过程均值或目标值)
绘制控制图:时间轴为横轴,统计量为纵轴,标注UCL、CL、LCL。
分析异常:
点超出界限:立即调查。
趋势/模式:如连续7点上升、周期性波动等,提示过程偏移。
示例:以X̄-R图为例
数据收集:
子组大小通常4-5,组数≥25。
示例:每小时取5个零件测直径(mm):
子组1: 10.2, 10.1, 10.3, 10.0, 10.2
子组2: 10.4, 10.3, 10.2, 10.5, 10.3
...
计算统计量:
X̄(子组均值)= (10.2+10.1+10.3+10.0+10.2)/5 = 10.16
R(子组极差)= max(10.2,10.1,10.3,10.0,10.2) - min(...) = 0.3
确定控制限:
总均值X̄̄ = 所有X̄的平均值
平均极差R̄ = 所有R的平均值
UCL_X̄ = X̄̄ + A₂·R̄ (A₂查表,n=5时为0.577)
LCL_X̄ = X̄̄ - A₂·R̄
UCL_R = D₄·R̄ (D₄=2.114)
绘图分析:
标记中心线、控制限,绘制X̄和R点序列。
检查是否出现8种异常模式。
判异准则与注意事项
判异准则
超出控制限:单点超出UCL/LCL(过程失控)。
连续7点同侧:可能均值偏移(如设备校准失效)。
连续6点递增/递减:趋势性变化(如刀具磨损)。
连续14点上下交替:系统性干扰(如两班次操作差异)。
2/3点落在A区外:A区=±2σ范围(预警信号)。
连续15点在C区:C区=±1σ范围(过度控制或数据造假)。
连续8点无C区:分层现象(如混合多批原材料)。
周期性波动:固定间隔异常(如设备定期故障)。
使用要点
数据准确性:确保采集设备校准,避免人为误差。
动态调整:过程稳定后需重新计算控制限。
整合工具:
与直方图结合分析数据分布形态;
嵌入六西格玛DMAIC框架,在"控制阶段"固化改进。
应用场景
制造业
监控关键参数(如零件尺寸、温度),实时报警设备偏差,减少废品率。
案例:汽车厂通过X̄-R图控制喷漆厚度,及时调整设备参数。
服务业与医疗
追踪患者等待时间、手术并发症率,优化服务流程。
案例:医院用P图监控护理投诉率,针对性培训后满意度提升。
金融与教育
分析投资组合波动、学生成绩趋势,辅助风险决策与教学改进。
研发领域
识别实验数据异常值,确保研发过程稳定性。
优势与局限
优势:
直观展示过程状态,支持数据驱动决策。
预防质量问题,减少事后返工成本。
局限:
依赖数据准确性,需定期校准测量系统。
无法直接识别具体原因,需结合其他工具(如鱼骨图、5Why分析)。
实践建议
选择合适图表:根据数据类型(连续/离散)和样本量选择控制图。
持续更新:定期收集新数据,重新计算控制界限以反映过程改进。
培训团队:确保操作人员理解判异规则,避免误判。
结合其他工具:与SPC(统计过程控制)、六西格玛等方法结合使用。
示例:某汽车零部件厂使用X-bar & R图监控轴径尺寸,发现连续7点低于中心线,调查后发现磨具磨损,及时更换后过程恢复稳定。
通过合理应用控制图,企业可实现从“事后检验”到“事前预防”的转变,显著提升质量与效率。
控制图 vs 趋势图
| 对比项 | 控制图 | 趋势图 |
|---|---|---|
| 核心目的 | 区分普通/特殊原因变异,监控过程稳定性 | 单纯展示数据随时间变化趋势 |
| 控制限 | 基于统计学计算(±3σ) | 无标准限制,可自定义阈值 |
| 适用场景 | 生产过程质量管控 | 销售数据、温度记录等描述性分析 |
常见问题解答
Q1:控制限能否调整?
原则上不可随意更改,除非过程改进后重新计算(如六西格玛项目后标准差缩小)。
Q2:数据不服从正态分布怎么办?
使用非参数控制图(如中位数图)或进行数据变换(如Box-Cox变换)。
Q3:控制图发现异常后如何处理?
立即排查特殊原因(如原材料批次、设备故障),消除后重新收集数据计算控制限。
工具推荐
软件:Minitab(SPC专业分析)、JMP、Excel(需手动公式)
模板:
# Python示例(使用numpy和matplotlib)
import numpy as np
import matplotlib.pyplot as plt
data = np.random.normal(50, 2, 100) # 均值50,标准差2的100个数据
mean, std = np.mean(data), np.std(data)
plt.plot(data, 'bo-')
plt.axhline(mean, color='g', label='CL')
plt.axhline(mean + 3*std, color='r', linestyle='--', label='UCL')
plt.axhline(mean - 3*std, color='r', linestyle='--', label='LCL')
plt.legend()
plt.show()
总结
控制图是质量管理的“心电图”,通过量化波动实现预防性管控。掌握其原理和判异规则,可显著降低过程变异,提升产品一致性。
控制图是企业实现预防性质量管理的基石,其核心价值在于实时预警异常而非事后检验。成功应用需结合场景选择类型、严格执行制作步骤、动态响应异常信号,并与其他质量工具(如PDCA循环)协同。随着工业4.0发展,控制图正与大数据分析、AI预测结合,迈向智能化实时监控的新阶段。